- Journal Home
- Volume 38 - 2025
- Volume 37 - 2024
- Volume 36 - 2023
- Volume 35 - 2022
- Volume 34 - 2021
- Volume 33 - 2020
- Volume 32 - 2019
- Volume 31 - 2018
- Volume 30 - 2017
- Volume 29 - 2016
- Volume 28 - 2015
- Volume 27 - 2014
- Volume 26 - 2013
- Volume 25 - 2012
- Volume 24 - 2011
- Volume 23 - 2010
- Volume 22 - 2009
- Volume 21 - 2008
- Volume 20 - 2007
- Volume 19 - 2006
- Volume 18 - 2005
- Volume 17 - 2004
- Volume 16 - 2003
- Volume 15 - 2002
- Volume 14 - 2001
- Volume 13 - 2000
- Volume 12 - 1999
- Volume 11 - 1998
- Volume 10 - 1997
- Volume 9 - 1996
- Volume 8 - 1995
- Volume 7 - 1994
- Volume 6 - 1993
- Volume 5 - 1992
- Volume 4 - 1991
- Volume 3 - 1990
- Volume 2 - 1989
- Volume 1 - 1988
Cited by
- BibTex
- RIS
- TXT
In this paper, we study the asymptotic behavior of solutions to a quasilinear
two-species chemotaxis system with nonlinear sensitivity and nonlinear signal production
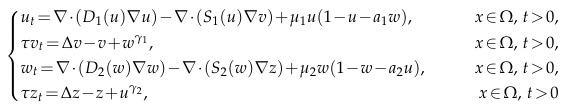
under homogeneous Neumann boundary conditions in a smooth bounded domain $Ω⊂\mathbb{R}^n(n≥2)$ where the parameter $\mu_1,\mu_2,γ_1,γ_2$ are positive constants, $τ ∈ \{0,1\}.$ The diffusion coefficients $D_i,Si ∈ C^2([0,∞))$ satisfy $D_i(s)≥a_0(s+1)^{−m_i},$ $0≤S_i(s)≤
b_0s(s+1)^{β_i−1},$ $s≥0,$ $m_i,β_i ∈\mathbb{R},$ $a_0,b_0 >0,$ $i=1,2.$ Under the assumption of properly
initial data regularity, we can find appropriate $\mu_i$ such that the globally bounded solution of this system satisfies the following relationship.
(I) If $a_1,a_2∈(0,1)$ and $\mu_1$ and $\mu_2$ are sufficiently large, then any globally bounded solution exponentially converges to $(\frac{1-a_1}{1-a_1a_2}, (\frac{1-a_2}{1-a_1a_2})^{\gamma_1}, \frac{1-a_2}{1-a_1a_2}, (\frac{1-a_1}{1-a_1a_2})^{\gamma_2})$ as $t→∞;$
(II) If $a_1 >1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
exponentially converges to (0,1,1,0) as $t→∞;$
(III) If $a_1=1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
algebraically converges to (0,1,1,0) as $t→∞.$
In this paper, we study the asymptotic behavior of solutions to a quasilinear
two-species chemotaxis system with nonlinear sensitivity and nonlinear signal production
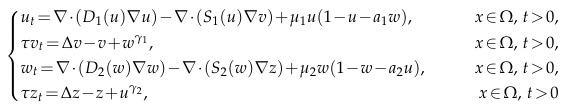
under homogeneous Neumann boundary conditions in a smooth bounded domain $Ω⊂\mathbb{R}^n(n≥2)$ where the parameter $\mu_1,\mu_2,γ_1,γ_2$ are positive constants, $τ ∈ \{0,1\}.$ The diffusion coefficients $D_i,Si ∈ C^2([0,∞))$ satisfy $D_i(s)≥a_0(s+1)^{−m_i},$ $0≤S_i(s)≤
b_0s(s+1)^{β_i−1},$ $s≥0,$ $m_i,β_i ∈\mathbb{R},$ $a_0,b_0 >0,$ $i=1,2.$ Under the assumption of properly
initial data regularity, we can find appropriate $\mu_i$ such that the globally bounded solution of this system satisfies the following relationship.
(I) If $a_1,a_2∈(0,1)$ and $\mu_1$ and $\mu_2$ are sufficiently large, then any globally bounded solution exponentially converges to $(\frac{1-a_1}{1-a_1a_2}, (\frac{1-a_2}{1-a_1a_2})^{\gamma_1}, \frac{1-a_2}{1-a_1a_2}, (\frac{1-a_1}{1-a_1a_2})^{\gamma_2})$ as $t→∞;$
(II) If $a_1 >1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
exponentially converges to (0,1,1,0) as $t→∞;$
(III) If $a_1=1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
algebraically converges to (0,1,1,0) as $t→∞.$
