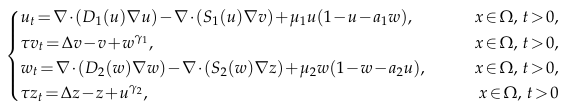
In this paper, we study the asymptotic behavior of solutions to a quasilinear
two-species chemotaxis system with nonlinear sensitivity and nonlinear signal production
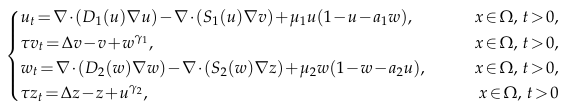
under homogeneous Neumann boundary conditions in a smooth bounded domain $Ω⊂\mathbb{R}^n(n≥2)$ where the parameter $\mu_1,\mu_2,γ_1,γ_2$ are positive constants, $τ ∈ \{0,1\}.$ The diffusion coefficients $D_i,Si ∈ C^2([0,∞))$ satisfy $D_i(s)≥a_0(s+1)^{−m_i},$ $0≤S_i(s)≤
b_0s(s+1)^{β_i−1},$ $s≥0,$ $m_i,β_i ∈\mathbb{R},$ $a_0,b_0 >0,$ $i=1,2.$ Under the assumption of properly
initial data regularity, we can find appropriate $\mu_i$ such that the globally bounded solution of this system satisfies the following relationship.
(I) If $a_1,a_2∈(0,1)$ and $\mu_1$ and $\mu_2$ are sufficiently large, then any globally bounded solution exponentially converges to $(\frac{1-a_1}{1-a_1a_2}, (\frac{1-a_2}{1-a_1a_2})^{\gamma_1}, \frac{1-a_2}{1-a_1a_2}, (\frac{1-a_1}{1-a_1a_2})^{\gamma_2})$ as $t→∞;$
(II) If $a_1 >1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
exponentially converges to (0,1,1,0) as $t→∞;$
(III) If $a_1=1>a_2 >0$ and $\mu_2$ is sufficiently large, then any globally bounded solution
algebraically converges to (0,1,1,0) as $t→∞.$