Cited by
Let $\Omega$ be a domain with a hole containing the origin in $\mathbb{R}^2$ and $u$ be a solution
to the problem
where $\partial^{\pm}\Omega$ represents the outer and inner boundaries of $\Omega,$ respectively, $c$ is a constant.
Let ${\mu}_k$ denote the $k{\rm th}$ Neumann eigenvalue of the Laplacian on $\Omega$ and${\Omega}_h$ is the hole.
We establish that if $\mu< {\mu}_8,$ then $\Omega$ is an annulus.
- BibTex
- RIS
- TXT
Let $\Omega$ be a domain with a hole containing the origin in $\mathbb{R}^2$ and $u$ be a solution
to the problem
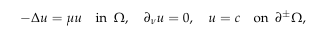
where $\partial^{\pm}\Omega$ represents the outer and inner boundaries of $\Omega,$ respectively, $c$ is a constant.
Let ${\mu}_k$ denote the $k{\rm th}$ Neumann eigenvalue of the Laplacian on $\Omega$ and${\Omega}_h$ is the hole.
We establish that if $\mu< {\mu}_8,$ then $\Omega$ is an annulus.
Let $\Omega$ be a domain with a hole containing the origin in $\mathbb{R}^2$ and $u$ be a solution
to the problem
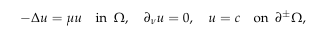
where $\partial^{\pm}\Omega$ represents the outer and inner boundaries of $\Omega,$ respectively, $c$ is a constant.
Let ${\mu}_k$ denote the $k{\rm th}$ Neumann eigenvalue of the Laplacian on $\Omega$ and${\Omega}_h$ is the hole.
We establish that if $\mu< {\mu}_8,$ then $\Omega$ is an annulus.