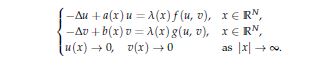On Non-Linearly Coupled Schrodinger Systems
Jing Zhang
Anal. Theory Appl. DOI: 10.4208/ata.OA-2025-0014
Publication Date : 2025-09-15