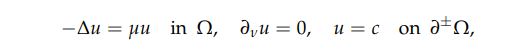A Rigidity Result for the Schiffer Conjecture on Domain with a Hole
Yingxin Sun
Anal. Theory Appl. DOI: 10.4208/ata.OA-2024-0023
Publication Date : 2025-06-16