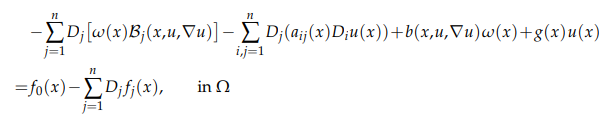We investigate non-traveling wave solutions of the (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation with time-dependent coefficients, which describes
the propagation of waves in incompressible fluids. We creatively combine the extended three-wave method with the generalized variable separation method and successfully obtain sixty exact non-traveling solutions including kink-like solutions, singular solitary wave-like solutions, periodic solitary wave-like solutions, periodic kink-like solutions, periodic cross-kink-like waves, homoclinic breather wave-like solutions
and so on. The variable coefficients and arbitrary functions in the obtained solutions
are easy to exhibit abundant soliton structures, which may be of great significance
for explaining some practical physical phenomena. By contour plots, 2D plots, and
3D plots, we analyze the dynamic characteristics of periodic cross-kink-like solution,
singular solitary wave-like solution, homoclinic breather wave-like solution. Additionally, we show changes of solutions under different tails to illustrate the influence
of tails on solutions.