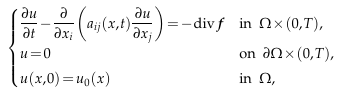In this note, we consider the following degenerate parabolic equation studied in [F. Chiarenza and R. Serapioni, Degenerate parabolic equations and Harnack inequality, Ann. Mat. Pura Appl. 137 (1984)] i.e.,

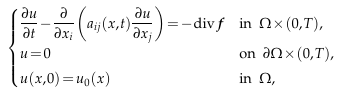
where $f=(f^1,···,f^n)$ and $Ω$ is a bounded domain in $\mathbb{R}^n$ with Lipschitz boundary, $n≥2$ and $T>0.$ In this paper, we apply Moser iteration argument to build up the explicit relationship among the coefficients $a_{i,j}(x,t)$, $f$ and the maximum norm of the solution. Meanwhile, we also find that the weighed Lebesgue space $L^{2l/(l−1)}$ to which $f$ belongs is essentially sharp in order to establish local boundedness of the solution. Here the definition of $l$ is found in Lemma 2.3. Our results cover the well-known results.

In this paper, we give the definitions of the non-self-adjoint spectral triple and its spectral Einstein functional. We compute the spectral Einstein functional associated with the nonminimal de Rham-Hodge operator on even-dimensional compact manifolds without boundary. Finally, several examples of the non-self-adjoint spectral triple are listed.

In this paper, we investigate the dynamical stability of transonic shock solutions for the full compressible Euler system in a two dimensional nozzle with a symmetric divergent part. Building upon the existence and uniqueness results for steady symmetric transonic shock solutions to the non-isentropic Euler system established in [Z.P. Xin and H.C. Yin, The transonic shock in a nozzle, 2-D and 3-D complete Euler systems, J. Differential Equations 245 (2008)], we prove the dynamical stability of the transonic shock solutions under small perturbations. More precisely, if the initial unsteady transonic flow is located in the symmetric divergent part of the nozzle and the flow is a symmetric small perturbation of the steady transonic flow, we use the characteristic method to establish the dynamical stability.