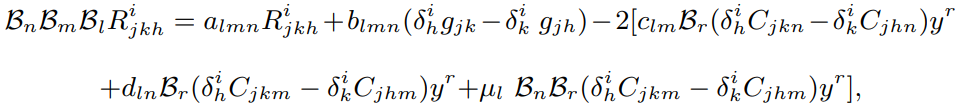
In this paper, we present a novel class of relations and investigate
the connection between the ${\rm R}$-projective curvature tensor and other tensors of
Finsler space $F_n.$ This space is characterized by the property for Cartan’s the
third curvature tensor $R^i_{jkh}$ which satisfies the certain relationship with given
covariant vectors field, as follows:
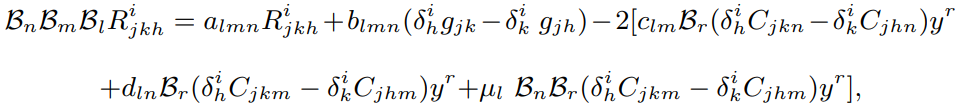
where $R^i_{jkh}\neq 0$ and $\mathcal{B}_n\mathcal{B}_m\mathcal{B}_l$ is the Berwald's third order covariant derivative with respect to $x^l,$ $x^m$ and $x^n$ respectively. The quantities $a_{lmn}= \mathcal{B}_nu_{lm} + u_{lm}\ λ_n,$ $b_{lmn} = \mathcal{B}_nv_{lm}+u_{lm} \ \mu_n,$ $c_{lm} = v_{lm},$ and $d_{ln} =\mathcal{B}_n\mu_l$ are
non-zero covariant vector fields. We define this space a generalized $\mathcal{BR}-3rd$ recurrent space and denote it briefly by $\mathcal{GBR}-3RF_n.$ This paper aims to derive
the third-order Berwald covariant derivatives of the torsion tensor $H^i_{kh}$ and the
deviation tensor $H^i_h.$ Additionally, it demonstrates that the curvature vector $K_j,$ the curvature vector $H_k,$ and the curvature scalar $H$ are all non-vanishing
within the considered space. We have some relations between Cartan’s third
curvature tensor $R^i_{jkh}$ and some tensors that exhibit self-similarity under specific conditions. Furthermore, we have established the necessary and sufficient
conditions for certain tensors in this space to have equal third-order Berwald
covariant derivatives with their lower-order counterparts.