Commun. Math. Anal. Appl., 4 (2025), pp. 307-335.
Published online: 2025-09
Cited by
The paper addresses the doubly elliptic eigenvalue problem
where $Ω$ is a bounded open subset of $\mathbb{R}^N$ $(N ≥ 2)$ with a $C^1$ boundary $Γ = Γ_0∪Γ_1,$ $Γ_0∩Γ_1 = ∅,$ $Γ_1$ being nonempty and relatively open on $Γ.$ Moreover, $\mathcal{H}^{N-1}(\overline{\Gamma}_0 \cap \overline{\Gamma}_1)=0$ and $\mathcal{H}^{N−1} (Γ_0) > 0.$ We prove that $L^2 (Ω)×L^2 (Γ_1)$ admits a Hilbert basis constituted by eigenfunctions and we describe the behavior of the eigenvalues. Moreover, when $Γ$ is at least $C^2$ and $\overline{Γ}_0∩\overline{Γ}_1=∅,$ we give several qualitative properties of the eigenfunctions.
- BibTex
- RIS
- TXT
The paper addresses the doubly elliptic eigenvalue problem
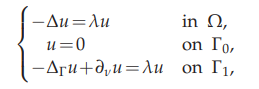
where $Ω$ is a bounded open subset of $\mathbb{R}^N$ $(N ≥ 2)$ with a $C^1$ boundary $Γ = Γ_0∪Γ_1,$ $Γ_0∩Γ_1 = ∅,$ $Γ_1$ being nonempty and relatively open on $Γ.$ Moreover, $\mathcal{H}^{N-1}(\overline{\Gamma}_0 \cap \overline{\Gamma}_1)=0$ and $\mathcal{H}^{N−1} (Γ_0) > 0.$ We prove that $L^2 (Ω)×L^2 (Γ_1)$ admits a Hilbert basis constituted by eigenfunctions and we describe the behavior of the eigenvalues. Moreover, when $Γ$ is at least $C^2$ and $\overline{Γ}_0∩\overline{Γ}_1=∅,$ we give several qualitative properties of the eigenfunctions.
The paper addresses the doubly elliptic eigenvalue problem
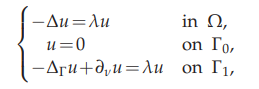
where $Ω$ is a bounded open subset of $\mathbb{R}^N$ $(N ≥ 2)$ with a $C^1$ boundary $Γ = Γ_0∪Γ_1,$ $Γ_0∩Γ_1 = ∅,$ $Γ_1$ being nonempty and relatively open on $Γ.$ Moreover, $\mathcal{H}^{N-1}(\overline{\Gamma}_0 \cap \overline{\Gamma}_1)=0$ and $\mathcal{H}^{N−1} (Γ_0) > 0.$ We prove that $L^2 (Ω)×L^2 (Γ_1)$ admits a Hilbert basis constituted by eigenfunctions and we describe the behavior of the eigenvalues. Moreover, when $Γ$ is at least $C^2$ and $\overline{Γ}_0∩\overline{Γ}_1=∅,$ we give several qualitative properties of the eigenfunctions.