full
search.png

Search

close.png

Cancel

arrow
Volume 41, Issue 3
Liouville Type Theorems for a Class of General Parabolic Hessian Quotient Type Equations

Hui Liu, Ni Xiang & Lina Zheng

DOI: 10.4208/ata.OA-2025-0006

Anal. Theory Appl., 41 (2025), pp. 238-258.

Published online: 2025-09

Preview Purchase PDF 4 55

Cited by

google scholar semantic scholar
Export citation
  • Abstract

We first consider the a priori estimates to a class of general parabolic $(k,l)-$ Hessian quotient type equations of the form

36cca9c7cc11a690f7a735685385904.png

with $0{\le}1<k{\le}n.$ We derive that any $k-$admissible-monotone solution to

7272fa253479ab71a9656a5110b7a9c.png

or

7cde00a4f7b91e282a13e73df98782e.png

has interior gradient estimates and Pogorelov type estimates. As an application, we prove Liouville type theorems for these equations.

  • Keywords

Parabolic $(k,l)$-Hessian quotient type equations, Pogorelov type estimates, Liouville type theorems.

  • AMS Subject Headings

35K55, 35B45, 35B08

  • Copyright

COPYRIGHT: © Global Science Press

  • Email address
  • BibTex
  • RIS
  • TXT
@Article{ATA-41-238, author = {Liu , HuiXiang , Ni and Zheng , Lina}, title = {Liouville Type Theorems for a Class of General Parabolic Hessian Quotient Type Equations}, journal = {Analysis in Theory and Applications}, year = {2025}, volume = {41}, number = {3}, pages = {238--258}, abstract = {

We first consider the a priori estimates to a class of general parabolic $(k,l)-$ Hessian quotient type equations of the form

36cca9c7cc11a690f7a735685385904.png

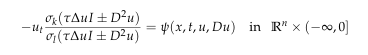
with $0{\le}1<k{\le}n.$ We derive that any $k-$admissible-monotone solution to

7272fa253479ab71a9656a5110b7a9c.png

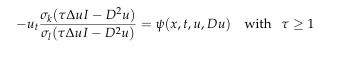
or

7cde00a4f7b91e282a13e73df98782e.png

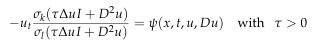
has interior gradient estimates and Pogorelov type estimates. As an application, we prove Liouville type theorems for these equations.

}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.OA-2025-0006}, url = {http://global-sci.org/intro/article_detail/ata/24485.html} }
TY - JOUR T1 - Liouville Type Theorems for a Class of General Parabolic Hessian Quotient Type Equations AU - Liu , Hui AU - Xiang , Ni AU - Zheng , Lina JO - Analysis in Theory and Applications VL - 3 SP - 238 EP - 258 PY - 2025 DA - 2025/09 SN - 41 DO - http://doi.org/10.4208/ata.OA-2025-0006 UR - https://global-sci.org/intro/article_detail/ata/24485.html KW - Parabolic $(k,l)$-Hessian quotient type equations, Pogorelov type estimates, Liouville type theorems. AB -

We first consider the a priori estimates to a class of general parabolic $(k,l)-$ Hessian quotient type equations of the form

36cca9c7cc11a690f7a735685385904.png

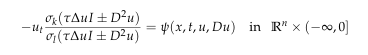
with $0{\le}1<k{\le}n.$ We derive that any $k-$admissible-monotone solution to

7272fa253479ab71a9656a5110b7a9c.png

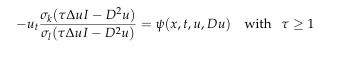
or

7cde00a4f7b91e282a13e73df98782e.png

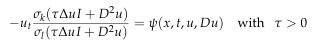
has interior gradient estimates and Pogorelov type estimates. As an application, we prove Liouville type theorems for these equations.

Liu , HuiXiang , Ni and Zheng , Lina. (2025). Liouville Type Theorems for a Class of General Parabolic Hessian Quotient Type Equations. Analysis in Theory and Applications. 41 (3). 238-258. doi:10.4208/ata.OA-2025-0006
Copy to clipboard
BibteX RIS TXT
The citation has been copied to your clipboard