Anal. Theory Appl., 37 (2021), pp. 209-229.
Published online: 2021-04
[An open-access article; the PDF is free to any online user.]
Cited by
- BibTex
- RIS
- TXT
The existence of an infinite sequence of sign-changing solutions are proved for a class of quasilinear elliptic equations under suitable conditions on the quasilinear coefficients and the nonlinearity
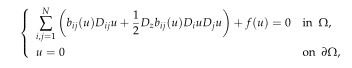
where $\Omega\subset\mathbb{R}^N$ is a bounded domain with smooth boundary, and we use
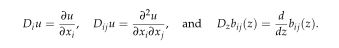
The main interest of this paper is for the case of bounded quasilinearity $b_{ij}$. The result is proved by an elliptic regularization method involving truncations of both $u$ and the gradient of $u$.
}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.2021.pr80.02}, url = {http://global-sci.org/intro/article_detail/ata/18772.html} }The existence of an infinite sequence of sign-changing solutions are proved for a class of quasilinear elliptic equations under suitable conditions on the quasilinear coefficients and the nonlinearity
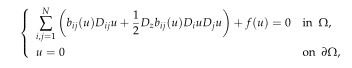
where $\Omega\subset\mathbb{R}^N$ is a bounded domain with smooth boundary, and we use
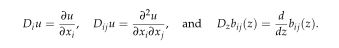
The main interest of this paper is for the case of bounded quasilinearity $b_{ij}$. The result is proved by an elliptic regularization method involving truncations of both $u$ and the gradient of $u$.
